Insulin and protein dynamics

Introduction

Insulin is perhaps one of the most well-studied proteins, and I don't say that lightly. It was the first protein to have its amino-acid sequence elucidated (an incredible achievement of biochemistry which led to Frederick Sanger winning the Nobel Prize in Chemistry in 1958) and one of the first to be solved by X-ray crystallography (by Dorothy Hodgkin, who also won a Nobel Prize in Chemistry for her role in the development of protein crystallography). Beyond its importance in the history of protein biochemistry, insulin also holds an essential role in the annals of medical history, given its connection to diabetes.

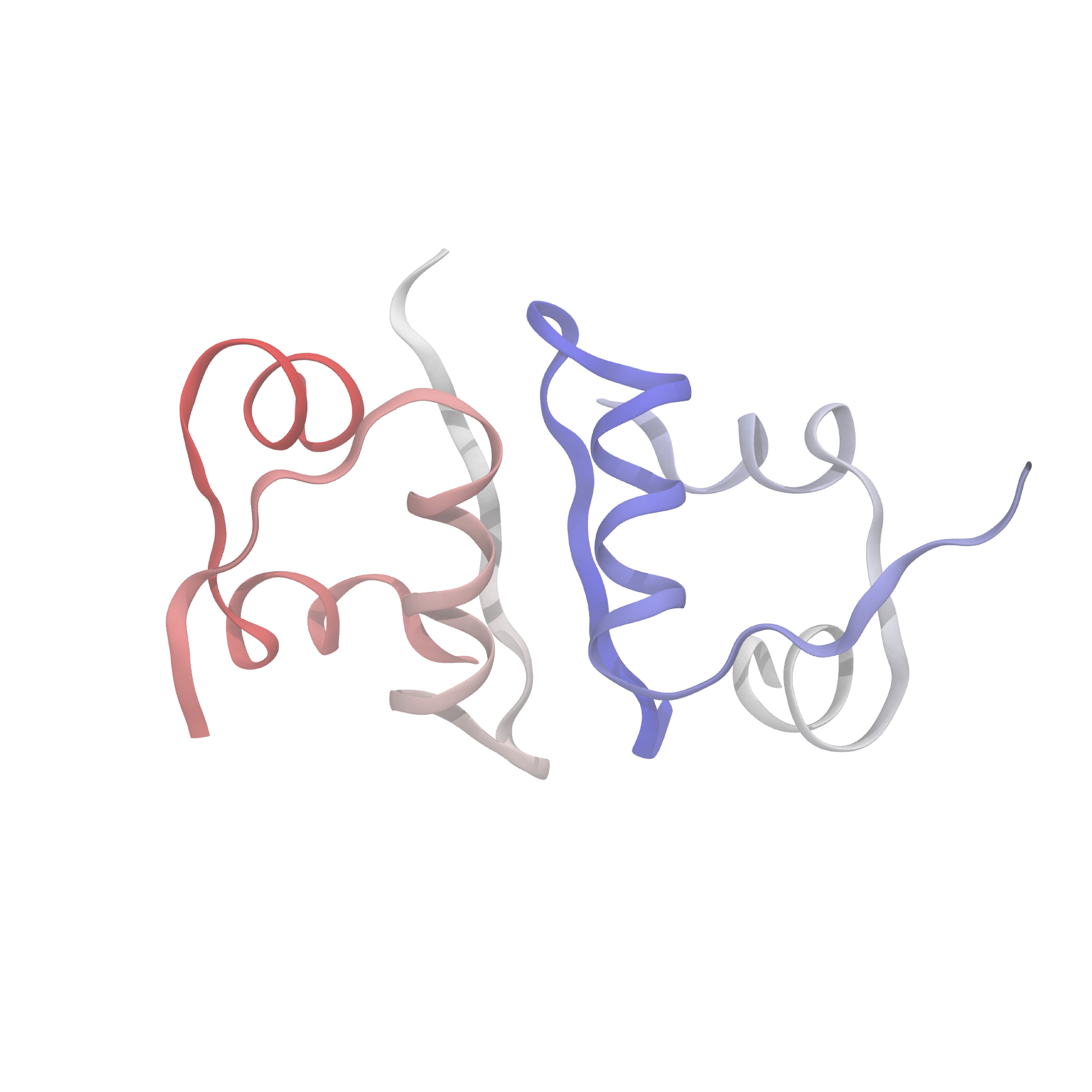
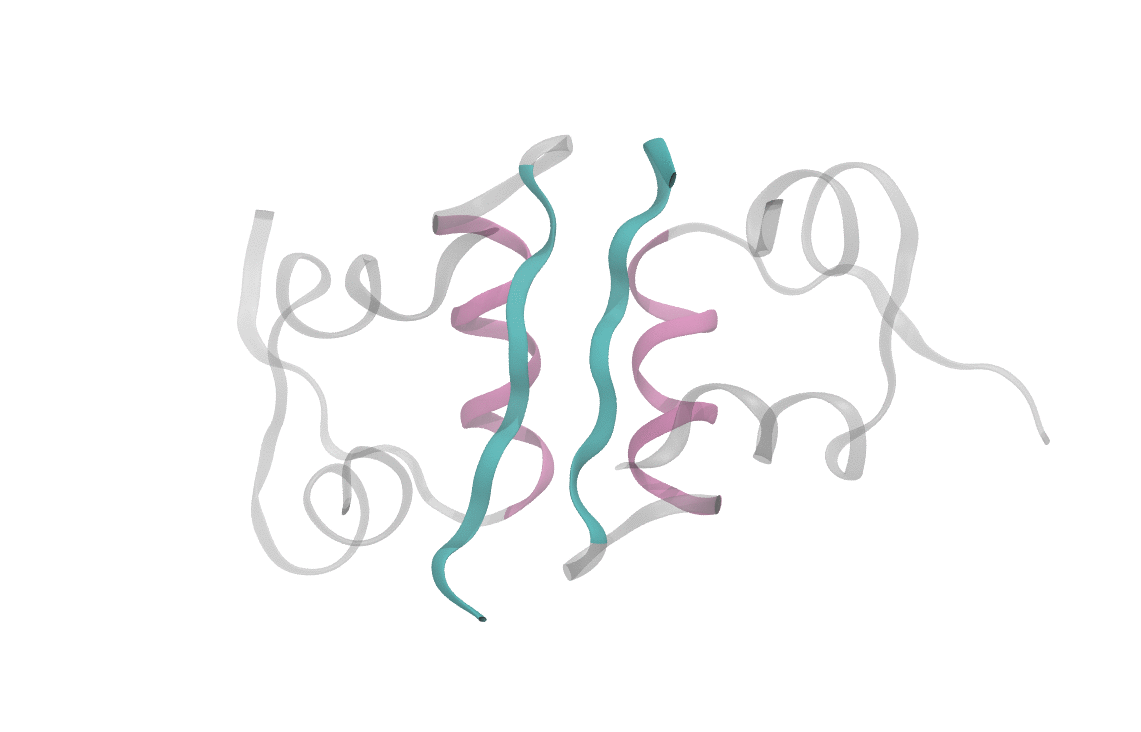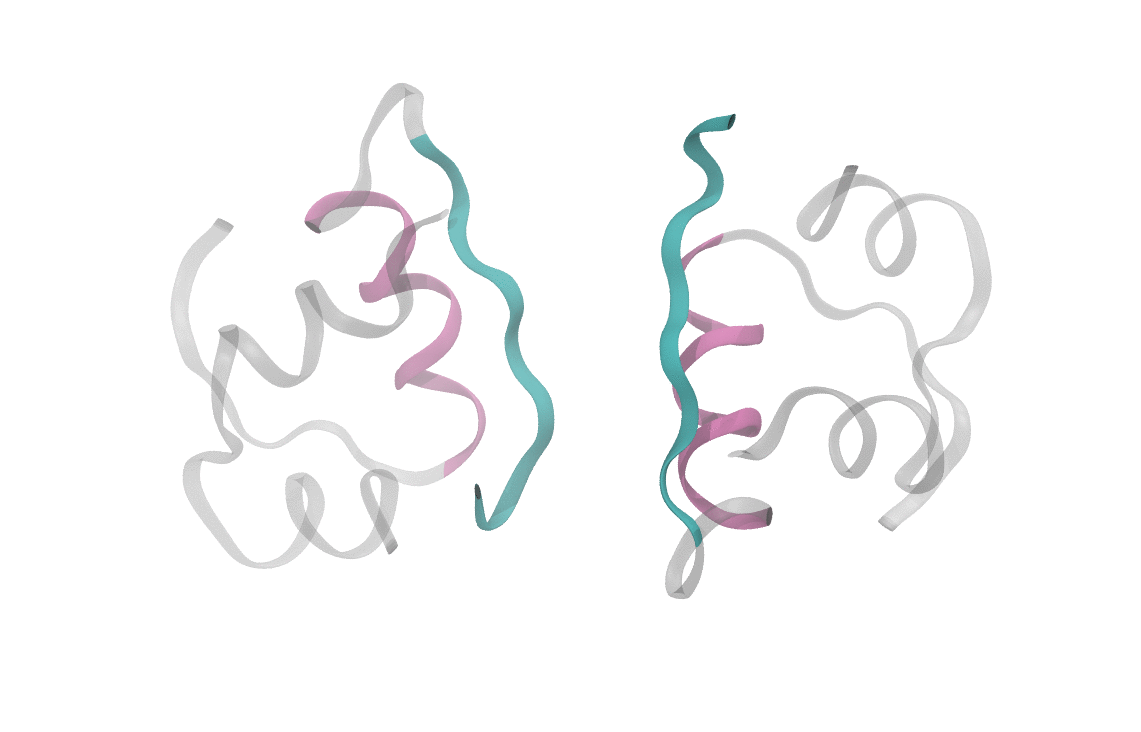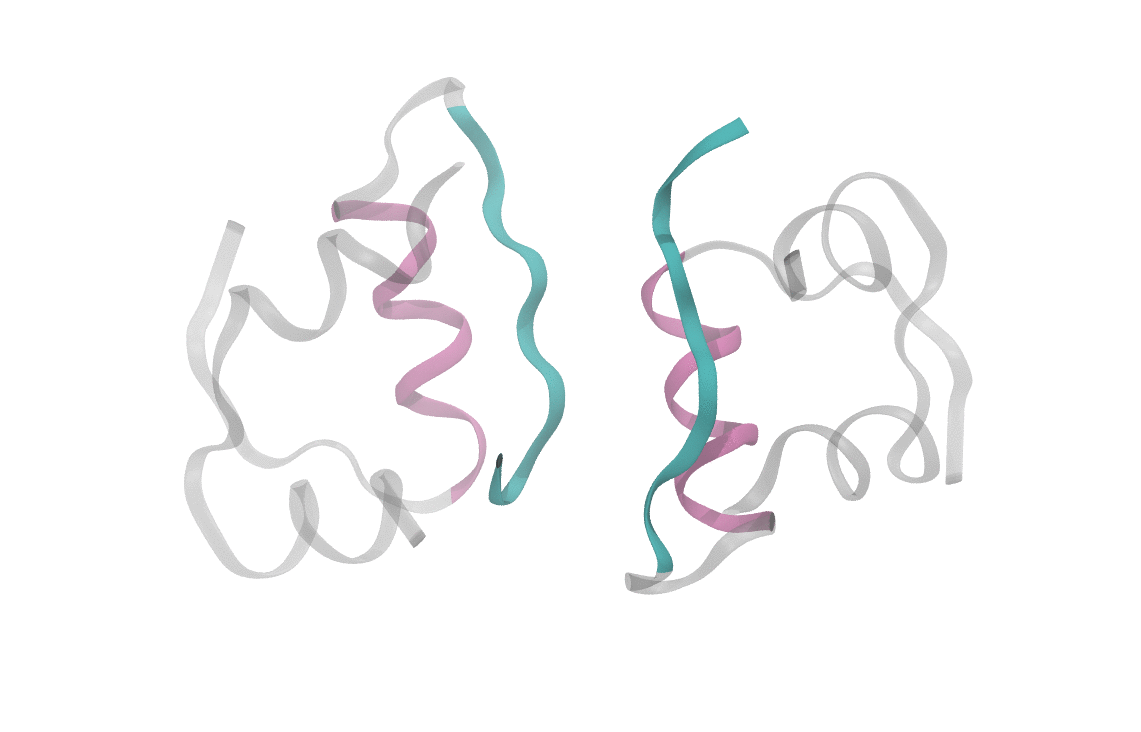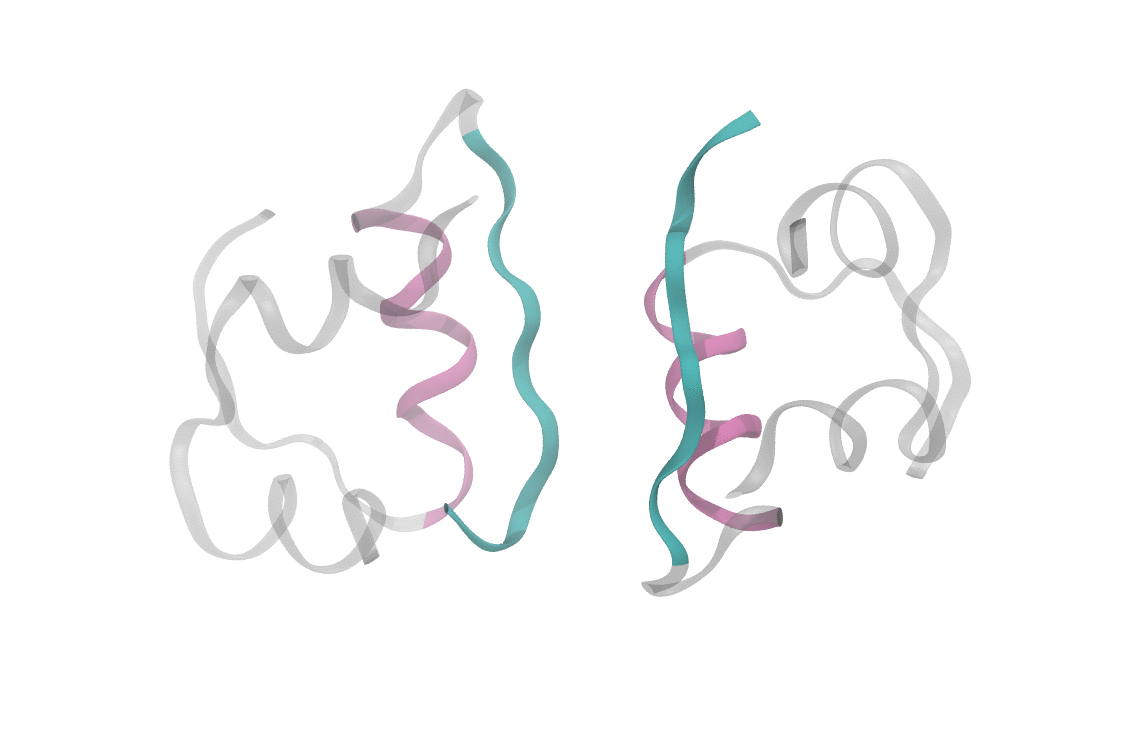
What's known today (and relevant for what I'll discuss here) is that the insulin molecule consists of two polypeptide chains, labeled A and B, with 21 and 30 amino acids, respectively. These two chains are held together by disulfide bridges between the A7-B7 and A20-B19 residues. Below is an image of the structure, displaying several secondary features of interest. Of particular note are the alpha-helices and beta sheets which form the monomer-monomer interface.

Figure 1: Structure of the insulin dimer.

In the body, insulin is stored as a hexamer, which dissociates first into dimers, and then into monomers, which are the active form that bind to insulin receptors. The equilibria between hexamer, dimer, and monomer turn out to be essential for maintaining the correct balance of active insulin in the blood, and hence many therapeutic formulations aim to alter these equilibria in predictable ways. For example, several fast-acting insulin variants destabilize the dimer in order to favor formation of the monomer. Despite the decades of pharmaceutical reserch on insulin and its therapeutic analogues, it's not entirely clear still how these variants actually affect the hexamer-dimer-monomer equilibria and hence the timescale of activity.

Dissocation and association

In many ways, the dissociation and association of insulin is a prototypical reaction in biochemistry: we frequently want to understand protein-protein interaction at both a macroscopic (e.g. binding coefficients) and microscopic scales (i.e., which residues are involved) In fact, the dissociation from insulin dimer to monomer is conceptually simple since it involves two partners which are identical, as well as an extremely well-studied protein system. Although the macroscopic features of insulin dimer dissociation can be (relatively) easily measured through experiments, the microscopic features are much more difficult to probe using conventional techniques.

At heart, we care about understanding the sequence of events which cause a dimeric insulin molecule to spontaneously separate and break into two monomers. This process, though simple enough that you could describe it in a sentence, requires many things to happen correctly all at once. Consider the animation below, which shows only the interfaces in color (the aforementioned beta sheet in cyan and the alpha helix in magenta). From this short movie, it's rather entirely unclear what is occuring as the two monomers move apart. Is it the specific motions of sidechains at the interface? Is it water molecules (not pictured here, but essential for any biological process) invading the monomer-monomer surface? These are the types of questions we seek to answer and that scientists have probed since the beginning of the structural era in biochemistry.

Figure 2: Animation of the insulin dimer dissociating. Each frame is 10 ps long and the entire trajectory captures about 1 ns of real time.

I mentioned earlier that designing experiments to investigate these aspects of protein-protein interaction can be very difficult—how does one differentiate between two competing pathways, for example, which might be present at the same time in a population of dimers? One possible way would be to mutate residues at the interface, one by one, and investigate their effects on the kinetics and/or thermodynamics of interaction. This might be difficult to interpret, however, given that data are noisy and extracting the correct information about what a given residue's role is often difficult when there are complex mechanisms or competing dynamics caused by mutation. Another potential method is to directly measure time-dependent changes using some kind of spectroscopic technique. We might envision applying something like NMR or infrared spectroscopy to ascertain the evolution of spectral features, which might in turn yield insight into structural changes of our protein. However, this turns out to be extremely challenging due to the difficulty in assigning spectra (for IR), limited time-resolution (in the case of NMR), and other related problems.

An entirely alternative method to these experiments is to perform a "computational" experiment, simulating our system using a computer and in principle revealing information at a much more detailed spatial and time-resolution. More specifically, a common method called molecular dynamics (see these slides for a nice non-technical overview), or MD, models the atomic dynamics by integrating Newton's equations of motion. Of course, when using a computer simulation, we must keep in mind that it is indeed a simulation, so it cannot perfectly model reality. In simulations of proteins, the empirical models we use to calculate forces on our molecules and the water molecules which surround them are parameterized imperfectly, and hence do not exactly reproduce all the behavior we might want.

Beyond the issues with incomplete modeling of physical reality, we must contend with the vast timescales of biological events compared with those of typical simulations. For atomistic MD simulations, the timestep (i.e. how much we integrate forward Newton's equations at every step) is limited to a few femtoseconds (1e-15 s).

The fundamental limitation for how long an MD timestep is the fastest vibrational motions in a system, which is around 1 femtosecond for an explicit atomistic simulation. Nowadays, there are several algorithms which can constrain the hydrogen atoms in a protein system, enabling slightly larger timesteps, but these are still peak around 4 femtoseconds. To do even better than this, we need to be more tricky with how we actually perform the integration (check out the BAOAB integrator) or by using multiple sizes of timesteps (e.g. the RESPA algorithm). With all these fancy tricks, we can in principle push the timestep up to around 8 femtoseconds (!).

On the other hand, many processes, including insulin dissociation, occur on the millisecond timescale or longer (hours for some ligand-protein dissociations). To directly observe a dissociation event would hence take approximately 1 trillion timesteps! Even with the fastest supercomputers available today, collecting adequate statistics would be unfeasible for any interesting event.

With those caveats aside, however, the advantages of MD simulations are that they yield an atomic level picture into whatever process we are studying. We can track the motion of every atom (in principle) at a resolution limited only by our timestep that in most cases runs much faster than any interesting events. Furthermore, computational simulations can be performed in any conditions we want, unburdened by the necessities of experiment. For example, insulin studies often require some amount of ethanol as co-solvent to prevent aggregation. The ethanol affects the electrostatic properties of the surrounding water medium, leading to different dissociation behavior. In a simulation, we can choose whatever pH, whatever salt concentration, whatever co-solvent, etc. we want. Now to be frank, all this is great and wonderful, but we still haven't addressed the timescale issue.

Long-timescale analysis

It turns out there's a pretty slick way of getting around the fact that we typically can (or want) to run a bunch of short simulations rather a single long simulation (how short depends on the actual system, but for our purposes, let's say anything less than a microsecond). Running a bunch of short simulations also lends itself well to the massively-parallel computer architectures you find in general-purpose supercomputers, where there's a bunch of cores packed into nodes without a ton of interconnection. With that in mind, here's the gist of it:

Here's a more technical description for those interested: the specific thing (mathematical object) that we are trying to approximate from our short trajectories is what's called the transition operator (or Koopman operator in the dynamical systems literature). This infinite-dimensional operator tells us how functions of a Markovian system evolve with time. Note that I emphasized functions. The transition operator doesn't propagate the actual coordinates forward, but rather functions of those coordinates. The useful thing about the transition operator is that its linear, so we can study its spectral properties. This turns out to underlie a bunch of techniques which people in the MD community have been using for many years, such as Markov state models (MSMs) and time-lagged independent components analysis (TICA). In short, we are trying to approximate the transition operator's action on certain functions that we like and tell us about the mechanism of our system. These approximations are essentially Monte Carlo estimates of the transition operator over the short trajectories, which can be in turn used to predict out to longer-time.

in order to study the dissociation or association process, what we really care about are the long-timescale dynamics of the system. That is, given some initial configuration of our insulin dimer, we want to know what its behavior sometime in the future likely will be (where that future is longer than the scale of our short trajectories). Even though we can't represent these long-timescale dynamics exactly, we can approximate them through our collection of short trajectories! That's the key idea, that we use our short trajectories as essentially a proxy for the "real" long-time evolution of the system, and then stitch them together a bunch of times to reconstruct what a long simulation might actually look like. The beautiful part about this is that we can run our short simulations starting from configurations that actually might do something interesting (e.g. structures where the dimer is partially dissociated), and we can ignore the tons of useless data we would get from running a really long trajectory, where we can't really control what the system ends up doing.

Performing this analysis on insulin reveals some rather interesting aspects of its dissocation. Most salient is the fact that dimer dissociation is multi-pathway, or it proceeds through multiple different mechanisms, in other words. Looking at the structure of insulin, one might postulate that there are two limiting regimes for dissociation: one where the alpha helices separate first, and one where the beta sheets separate first. These are indeed two of the pathways that appear in computational analysis, though we see a large range of intermediate pathways between the two limits. Water also plays a large role, hydrating interfacial residues as the dimer begins to separate and mediating the monomer formation. Finally, the insulin dimer occasionally rotates along the interface without completely separating, which often represents a preliminary state in dissociation.

Conclusion

There are many other things that I could say about insulin in particular, but the punchline is that dissociation is an extremely complex process requiring the concerted action of many atoms. Furthermore, these kinds of specific insights would have been incredibly difficult, if not impossible to extract from experiments. Of course, the natural next steps are to investigate other protein-protein systems to see if these same kinds of lessons hold true. Are all protein-protein association processes inherently heterogeneous? How does water mediate dynamics at protein-protein interfaces? These are all questions which are ripe for computational study.

Home | Science