During my last two years at Stanford, I was looking into some of the fascinating properties of water for my work in the Markland group.
Water is ubiquitous. It drives our global climate, it powers essential biological functions, it spawns civilizations, it feeds our species. And yet, it behaves particularly strangely, with its two hydrogens and single oxygen contributing to a wide variety of chemically useful properties.
One of the most illuminating methods of understanding water's properties is via infrared (IR) spectroscopy. IR spectroscopy excites vibrational modes, or the stretches and twists and bends of a flexible molecule. In a sense, one might think of these vibrational excitations as a dance, where the two O-H bonds flex in concert, each linked with the movements of the other (i.e. vibrational coupling).
Much work has been done on computational simulation of IR spectra, which would enable useful studies in aqueous enzyme environments, for example. It turns out that one can obtain the IR spectrum of a molecule by taking the Fourier-transform of its dipole autocorrelation function. Generally, these dipoles are obtained from molecular dynamics (MD) simulations, which is where my work comes in.
Traditionally, one performs classical MD simulations, in which molecules are most commonly treated as balls connected by springs and thus subject to harmonic potentials. Many force fields exist which attempt to model the jiggling behavior of these molecules, to varying degrees of success. In principle, one can simply integrate Newton's equations of motion to propagate the system forward in time. However, these force field-based methods are limited by the specific parameters used, and ignore electronic effects often essential for describing chemical behavior. In an ideal world, we would be able to perfectly calculate the electronic structure (i.e. the wavefunction) of our many-body system of interest, thus understanding perfectly its chemical properties; however, computional tools obviously limit the tractability of this approach. Nevertheless, in the past few decades, advancements in hardware arising primarily from Moore's law and better approaches towards calculating electronic structure have rendered ab initio molecular dyanmics (AIMD) feasible (here, ab initio refers to a first-principles approach which relies on quantum mechanical calculations).
Perhaps the most popular approach today employs density functional theory (DFT), which is given a lucid pedagogical introduction here. I won't go too much into the details, since they can be found in many places on the Internet, but the main thrust involves treating the ground-state energy of a molecule as a functional of the electron density (hence the name). Here a functional simply refers to something which takes in a function and outputs a number (e.g. a definite integral).
Despite its incredible utility and general performance on a wide range of chemical systems, DFT scales rather poorly with the system size, often making it a poor choice for larger molecules. This is where semi-empirical methods come in, and in my case, density functional tight-binding (DFTB) to be precise. Semi-empirical methods refer to a broad range of techniques which lie somewhat in between classical and quantum mechanical calculations. Generalizing slightly, they essentially maintain the wavefunction-based approach of quantum chemical calculations while reducing complexity by adding several empirically-determined parameters.
DFTB in particular is based off a Taylor-expansion of the DFT functional, and is given an illuminating pedagogical treatment here. Perhaps one of the more interesting and relevant aspects of DFTB is its use of "tight-binding" orbitals, as indicated by its name. The idea comes from computational physics, and essentially tight-binding refers to the use of a basis set (i.e. atomic orbitals) which is localized closely on the atoms themselves---that is, the electrons are bound closely to the atoms to which they belong and don't interact much with neighboring atoms. Because of its limited basis and use of parameterized terms, DFTB can runs an order of magnitude faster on equivalent-sized systems compared to DFT, which greatly increases its applicability to large systems of interest.
Now, back from that long tangent on electronic structure theory, we can return to the problem at hand---calculation the IR spectra of water. By running ab initio MD simulations using DFTB on a container full of water molecules (subject to various physical and simulation conditions---temperature, pressure, boundary conditions---which I won't touch on here, but are highly relevant when performing simulations in practice), we can propagate our system forward in time while also determining the charges on each of our molecules via the electronic densities. Then, we simply apply calculate the dipoles as \begin{equation} \vec{\mu} = \sum_i q_i\vec{r}_i \end{equation} where \(\vec{\mu}\) is the dipole vector, \(q_i\) is the charge on the \(i\)th particle, and \(\vec{r}_i\) is the position vector of that particle. One can show (something for another day, perhaps) that the IR absorption intensities are proportional to the dipole autocorrelation function (as mentioned earlier): \begin{equation} A(\omega) \propto \int_0^\infty \langle \vec{\mu}(t)\cdot\vec{\mu}(0) \rangle e^{-i\omega t} \,dt. \end{equation} And we're done!
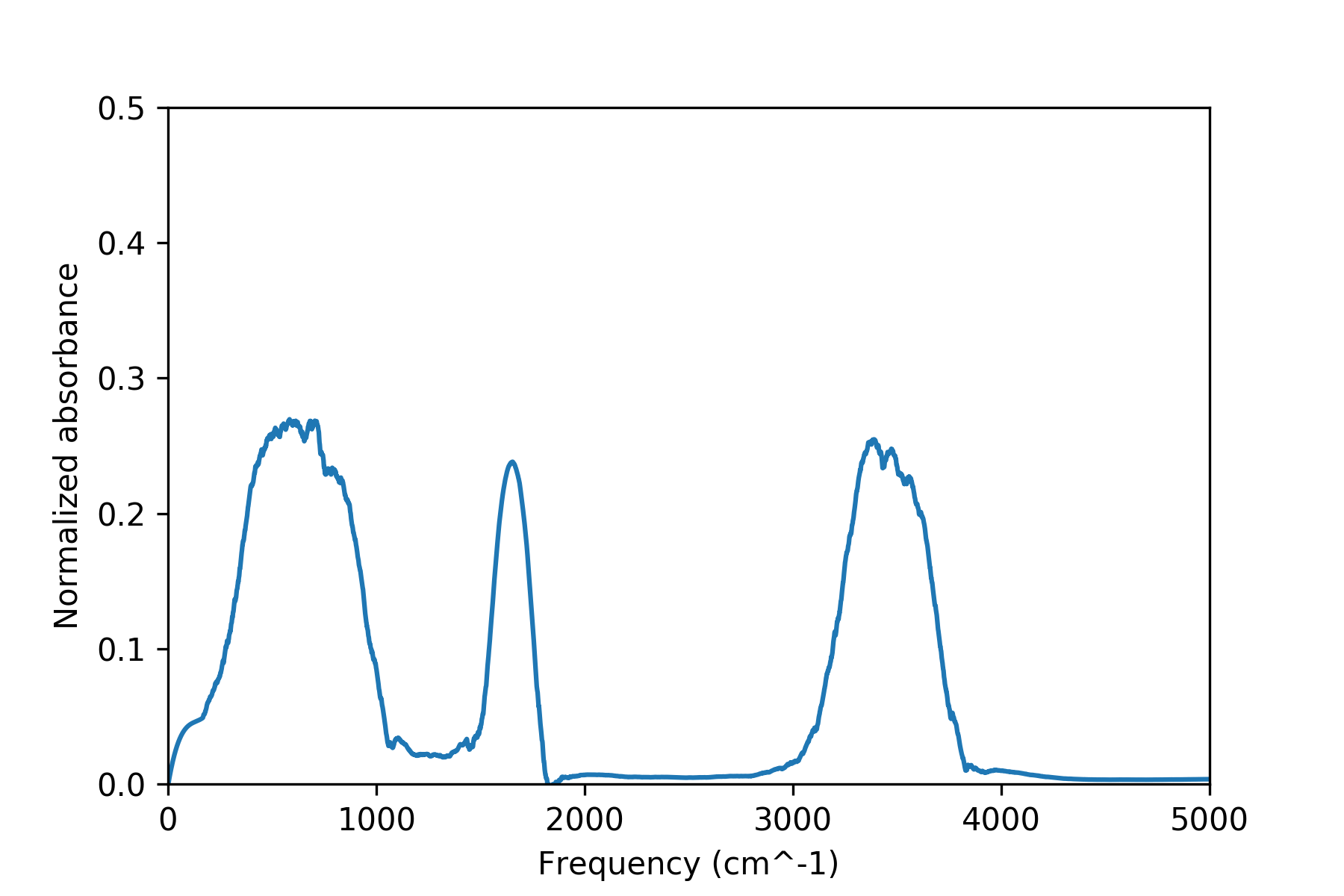
Here's a good idea of what the calculated spectrum looks like using DFTB (don't worry too much about the vertical axis, since the frequencies are generally more important and revealing):

It turns out that the large broad feature between 3000 and 4000 inverse centimeters (or around 100 THz/400 meV, for those physicists out there) corresponds to the stretching of the O-H bond in water. This peak features prominently in the IR spectra of anything which possesses an oxygen bonded to a hydrogen, and for that reason is rather useful for a quick analysis of many compounds. The peaks at lower frequencies (and hence energies) are other little bends and vibrations and jiggles of our water molecules.
Now, you might be thinking to yourself: wait, he didn't even tell me anything! This is just magic! And I wouldn't disagree with you. The first time I did this (using data computed with DFT), I thought it was magic, too. But of course it turns out there are many subtleties involved with the process. In fact, many researchers devote their entire careers to developing better methods for simulating various kinds of optical spectra (besides IR, you might want to simulate Raman spectra, UV-vis spectra, rotational spectra, etc.).